On the options markets, the so-called “Greeks” are the numerical indicators that traders use to measure the risks a particular type of trade entails. There are five main Greeks, each representing a specific variable: 

• Delta
• Gamma
• Vega
• Theta
• Rho

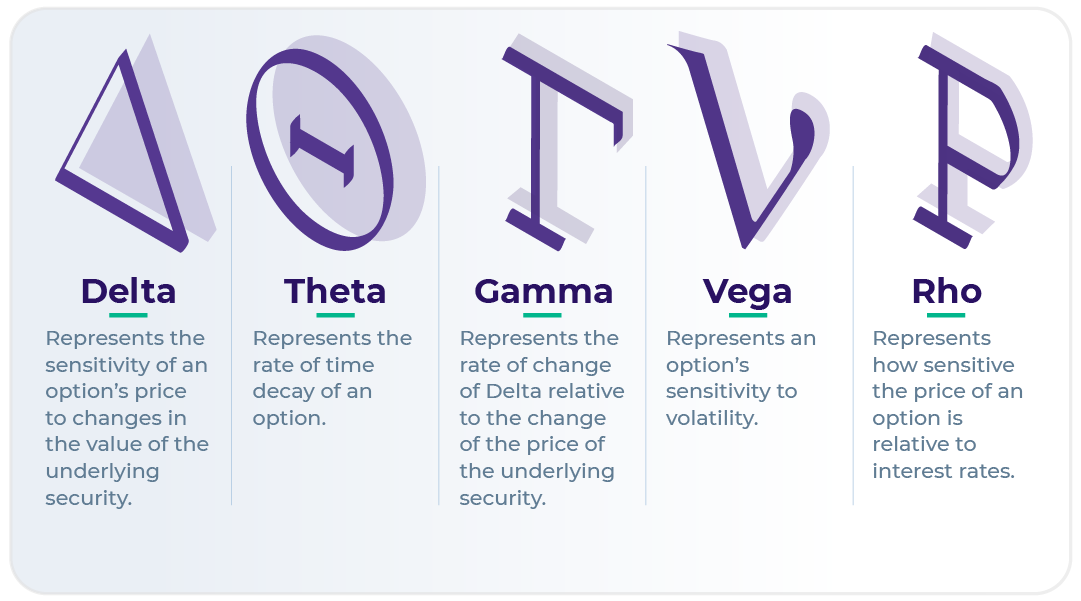
Delta ( Δ)

Delta tracks the value of an option relative to the underlying asset. This tells you whether an option will expire at the money, in the money, or out of the money. 

In a call option (an option to buy), Delta is a value between 0 and 1. Conversely, in a put option (an option to sell), Delta is a value between -1 and 0. 

Imagine you were thinking of buying an option to buy US Dollars in exchange for British Pounds at an exchange rate of 1.20. This means that, should you buy the option, it would give you the right to buy US Dollars at a rate of $1.20 for every £1. The option’s Delta is 0.75.

Delta of 0.75 means that the exchange rate available on the open market is lower than the exchange rate in the option. This means the option is in the money — you’ll get a better rate than you’d get on the open market. 

Conversely, Delta of 0.5 means the option is at the money, that is the exchange rate on the market and in the option are identical or very similar. And Delta closer to 0 means the option is out of the money — you’d get a better rate on the open market than you would by exercising the option.

Delta changes constantly. This reflects the fact that even strong currencies’ exchange rates fluctuate.

Gamma (Γ)

Gamma represents the rate of change in an option’s Delta over time. 

Gamma is typically highest when an option is at the money. This is because even a small fluctuation can affect the option’s value.

By contrast, Gamma is low when an option is in the money or out of the money. This is because, once an option is comfortably in or out of the money, its value is unlikely to change unless something unexpected happens. 

Using our previous example, if the option to buy US Dollars in exchange for British Pounds at an exchange rate of 1.20 is at the money, a small fluctuation of 0.1 either way can put you in the money or out of the money. So Gamma will be high. 

But if the open market exchange rate is 1.05, Gamma will likely be low. This is because the US Dollar and the Pound Sterling are both stable currencies, and a sudden 0.15 fluctuation is unlikely unless there’s a major, unforeseen event.

Vega (v)

Vega measures how sensitive an option is to volatility. 

Volatility is the rate at which the underlying asset fluctuates. High volatility means the underlying asset’s value can go from one extreme to another very quickly. Low volatility means the asset’s value is relatively stable. 

Options act like insurance. If the exchange rate becomes unfavourable, you can exercise the option to get a better rate. For this reason, volatility can have a huge impact on how much an option is worth. 

An option is more valuable when the underlying asset is volatile, because there’s a greater chance of extremes that could leave you out of pocket. 

In comparison, if volatility is low, there’s far less chance of sudden, unexpected changes. This means you’re less likely to need to exercise your option, so it’ll be worth less.

Theta (Θ)

Theta represents time-sensitivity. In other words, it tells you how much the price of an option will decrease over time. 

Theta’s value is tied to whether an option is at the money, in the money, or out of the money. At-the-money and out-of-the-money options’ Theta is higher the closer they get to their expiry date, because it becomes increasingly unlikely that the option will expire in the money. 

An in-the-money option, on the other hand, has lower Theta the closer it is to the expiry date. Barring a dramatic turn of events, such an option would likely be still in the money when it expires.

Rho (p)

Rho represents an option’s price sensitivity to interest rate shifts. 

While underlying assets — an emerging market’s currency, for instance — can be very volatile, interest rate fluctuations tend to be rarer, smaller, and take longer to have an effect — a shift of just 1% would probably cause a stir. 

For this reason, Rho tends to increase the further away an option’s expiry date is, while options that are about to expire will have Rho that is closer to zero.  

• Rho is the least important of the Greeks and not widely used when determining value and assessing risk. This is because interest rates tend to have a very minimal impact on options’ prices.
• Greeks are complicated to calculate, so traders typically use spreadsheets or leave the task to specialised software. Computer algorithms can continually work out the Greeks in real time.
• The Greeks get their name because they’re letters of the Greek alphabet. Or, well, four of them are. ‘Vega’ is a made up term, but the name ‘Greeks’ stuck, presumably because vega sounds like a Greek letter.

Want to know more?

• This in-depth guide walks you through the mathematical formulas used to work out the value of each Greek. It also shows you how you can calculate potential profit from options trading.
• If Rho is the least important Greek in options trading, Delta is by far the most important. This video explains it in more detail, including how it applies to call and put options.

Assure Hedge’s perspective:

“The Greeks are crucial when it comes to understanding whether an option will manage your risk effectively. But working them out and understanding what the numbers mean is rarely simple or straightforward. Options providers do all that hard work for you behind the scenes, so you can trade with confidence.”

Trading in leveraged financial instruments such as Options or other financial derivatives, carries a high level of risk and may not be suitable for all investors.  Investors who make use of these financial products run the risk of substantial capital losses which may exceed your initial deposit. Assure Hedge (UK) Limited makes no claim or warranty regarding either the appropriateness or suitability of these instruments for your purposes whether commercial or otherwise. Assure Hedge (UK) Limited may provide general commentary or educational material available on its website or otherwise, which is not intended as investment advice. You should carefully consider your financial situation and needs and seek independent advice from a duly authorised financial adviser. Assure Hedge (UK) Limited assumes no liability for errors, inaccuracies or omissions; does not warrant the accuracy, completeness of information, text, graphics, links or other items contained within these materials. You should read and understand Assure Hedge (UK) Limited’s Terms and Conditions prior to taking any further action.